-
ホーム
-
SPI非言語
-
グラフ・資料の読み取り
SPIのグラフ・資料の読み取りって何?
SPIのグラフ・資料の解析は、データを含むグラフや表を、正確に理解し、それに関する設問に答える問題です。
数値を理解する能力と、データを解釈する力が必要です。
とりわけ割合や増加率の計算が多い傾向です。
例えば、平均世帯人数を求める問題が出題されます。
正解するためには与えられたデータから情報を分析し、それに基づいて論理的な推論をすることです。
実際に問題パターンを見てみよう
グラフや資料を読み取る問題はどんな感じか、実際に問題に触れてみましょう。
問題
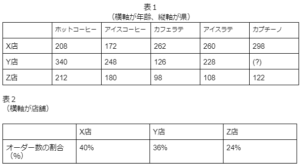
ある系列店のカフェX、Y、Zを訪れた客がオーダーしたドリンクを一定期間集計した。
表1はメニューごとに人数を集計したもの、表2は店舗X、Y、Zにおける各店舗のドリンクオーダー数の割合を示したものである。
表1の?に入る数字はいくらか。
解説を詳しく見る
X店のオーダーされたドリンクの総数は1,200でこれが全体の40%のオーダー数を占めるので、3店舗合計のドリンクオーダー総数は3,000。Y店舗のオーダー数は3000の36%で1,080。
1,080-340-248-126-228 = 138
グラフ・資料の読み取りに強くなるには
グラフや資料などのデータから答えを導くのが苦手な方もいるでしょう。
そんな方でも、対策をしておけば本番に強くなれます。
グラフや資料を読み解くには、データを正確に把握し、分析できる力が必要です。
まずは問題文をじっくり読み、必要な情報を正しく抽出しましょう。
また、データの比較や割合の計算をするための基本的なスキルも必要です。
さらに、問題文に隠されたヒントや条件を見逃さないようにしましょう。
問題文の情報を整理しよう
問題に取り組む際は、問題文の中にある情報をいったん整理しましょう。
このステップを丁寧におこなうことで、問題解決がより簡単になります。
情報を整理するには、まず問題文を注意深く読むことが基本です。
問題文の中に重要なデータやキーワード、条件がないか確認しましょう。
そして必要そうな情報は抽出することです。
例えば、距離、時間、速度、数値などは必要な情報である可能性が高いでしょう。
次に、これらの情報を視覚的に整理し、問題の構造を視覚的に理解しやすくします。
そのためにも図表やリストを作るといいでしょう。
その後、情報の関連性をつかみ、論理的に推論して問題解決を目指します。
問題文の条件下でどのように情報を適用するかを考え、解答を見つけましょう。
この段階では精密な計算や分析をおこなうことが大切です。
工夫して整理する
情報の整理の仕方を工夫しましょう。
そうすれば問題解決に向けて効果的にアプローチができます。
そのためにもまずは問題文をよく読み、関連するデータを出してください。
次にデータを視覚的に整理し、理解を深めていきます。
図や表を描くのもそうですが、情報を時系列で並べてみてもわかりやすいでしょう。
重要なデータには色をつけて強調するのも有効です。
これらの作業により、データ間の関係性が明白になり、論理的な思考がしやすくなります。
また、情報を分類するのも有益です。
例えば、数値データ、時系列データ、地理的データごとに分けて考えるのです。
問題の異なる側面が浮き彫りになり、さらに理解が深まるでしょう。
さらに、問題解決に必要な情報と不要な情報を区別するのも効果的です。
重要な情報だけに集中することで、効率的に答えを導けます。
問題文に含まれる複雑な情報を簡素にし、短い時間で問題に取り組むためにも必要なプロセスとなるでしょう。
尚、整理した情報を土台とし、段階的に問題を解決してください。
情報を整理するには、その情報が問題解決のプロセスにどのように関わるかを想定します。
そうすることで、情報の整理は単なる準備から問題解決の最終段階へと変わっていきます。
求めるべきものが何かを正確に把握する
何を求められているのかを正確に理解しましょう。
問題の核心に迫るには、やはり問題文を慎重に読むことです。
問題の主旨を正確に理解していなければ、非効率的になってしまいます。
文中のキーワードや特定の数値、条件に注意を払って読みましょう。
例えば、問題文に「最も効率的な」というフレーズがあるなら、最大や最小を求める問題である可能性が高いです。
そのため、グラフや表から得られる情報と問題文が求めている内容を結びつけ、どの情報が解答に直接影響するかを特定しましょう。
例えば、特定の年の売上を求める問題では、その年に関連するデータに注目します。
問題解決の過程で問題文が与えている条件や制限を考慮に入れ、それらが解答にどのように影響するか検討してください。
このように、問題が具体的に何を求めているのかを正確に理解し、それに基づいて論理的な推論をすることで、効果的に解けるでしょう。
例題を解く
表の読み取り002
X市、Y市、Z市の1年間の交通事故にあった人を数えた。
表1は年齢別に人数を集計したもの、表2はX、Y、Zにおけるそれぞれの事故にあった人の割合を示したものである。
19歳以上60歳未満が事故にあった割合が最も高い県を選べ。
例題:
A.X
B.Y
C.Z
D.表から読み取ることはできない
解説を詳しく見る
(?)に入る数を考える。
X市の事故にあった人数の総数は630人。これが全体の事故にあった割合の30%なので、X,Y,Z3つの市で事故にあった人数の合計は2100人とわかる。
これに33%をかけて、Y市の事故にあった人数の総数は693人、(?)に入るのは、329人とわかる。
さて、X市の19歳以上60歳未満の事故にあった人数は360人。割合は0.571で約57%
Y市の19歳以上60歳未満の事故にあった人数は88+329=417人。割合は0.601で約60%
Z市の19歳以上60歳未満の事故にあった人数は375人、事故にあった人数の総数は777人、割合は0.482で約48%
正解はY市である。
表の読み取り011
ある宅配便は、料金が荷物の大きさと重量によって決まっている。
一定の重量を超える荷物には超過料金が発生する。
運送料金は以下の2つの表の通りである。
Aさんはこれから4個の荷物を宅配便で配送する。
荷物の大きさと重量は以下の通り。
荷物A: 30cm, 22kg
荷物B: 50cm, 12kg
荷物C: 44cm, 30kg
荷物D: 170cm, 10kg
配送料金の合計金額を答えよ。
例題:
A. 4,020円
B. 4,125円
C. 4,220円
D. 5,025円
解説を詳しく見る
荷物A:420円
荷物B:800円
荷物C: 1,000円
荷物D: 1,800円
合計は4,020円












